L’enseignement des mathématiques et ce, dès la maternelle, vise à poser les bases d’une compréhension mathématique solide.
En effet, depuis de nombreuses années, les recherches en neurosciences tentent à prouver (B. Butterworth ; S. Dehaene) que le cerveau humain, dès la naissance, dispose de capacités mathématiques, notamment le sens du nombre. Il est donc nécessaire de stimuler, accompagner et structurer ces capacités dès le plus jeune âge.
Parmi les concepts fondamentaux, les motifs se distinguent par leur faculté à stimuler la pensée logique, algébrique et la créativité des enfants.
- La compréhension des motifs chez l’enfant[i]
Selon plusieurs études, les motifs sont perçus par le cerveau humain à travers des programmes mentaux abstraits (semblables à des instructions informatiques). Cette capacité à « compresser » l’information (par exemple, reconnaître une alternance croissante) est propre à l’humain, indépendamment du langage.
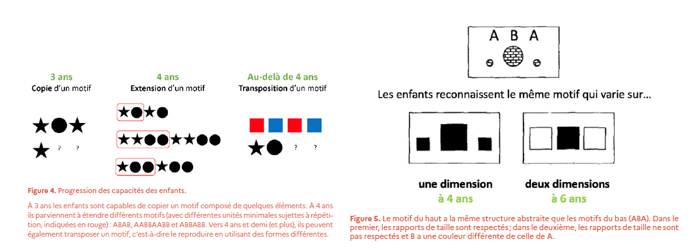
Dès la naissance, les enfants peuvent percevoir des séquences simples (visuelles, gestuelles et auditives), mais ce n’est qu’à partir de 3 ans qu’ils commencent à reconnaître et reproduire des motifs simples.
À 4 ans, ils parviennent à reproduire et généraliser des motifs plus complexes (comme ABAB ou AABBAABB), mais leur capacité d’abstraction reste limitée.
Ce n’est qu’à partir de 5-6 ans qu’ils deviennent capables de manipuler des motifs abstraits, indépendamment des variations de forme, de couleur ou de dimension.
La compréhension des motifs ne se limite pas aux motifs à répétitions simples. Elle s’applique aussi à ceux qui englobent également des séquences, des relations et des structures qui sont essentielles pour le raisonnement mathématique.
Les élèves sont capables d’établir la relation entre différentes représentations d’un même motif. Certains arrivent même à identifier et décrire explicitement l’unité de répétition.
Certaines recherches montrent que la compréhension des motifs est étroitement liée aux compétences visuo-spatiales et mathématiques.
On distingue deux sortes d’études :
- Études corrélationnelles : elles révèlent une relation entre la compréhension des motifs et des compétences comme le calcul, la proportion ou la mémoire visuo-spatiale.
- Études interventionnelles : elles suggèrent que l’entraînement aux motifs peut améliorer les compétences en mathématiques et en lecture, même si les résultats sont parfois variables.
Il s’agit donc, au-delà des capacités motrices et créatives, de voir quels sont les enjeux de l’étude des motifs à l’école primaire en mathématiques.
2. L’étude des motifs favorise la créativité mathématique
La créativité mathématique[ii] s’appuie sur l’idée que les Mathématiques ne se découvrent pas, elles se créent. Elle peut être alors définie comme une activité intellectuelle conduisant à la génération de nouvelles idées ou de réponses dans la résolution d’un problème mathématique. Cette activité se caractérise par :
- la capacité à générer de nombreuses idées,
- la capacité à aborder le problème de diverses perspectives,
- la capacité à produire des idées statistiquement peu fréquentes,
- dire la capacité d’approfondir les idées ou la situation initiale.
Dans le cadre d’une activité où il est demandé aux élèves de compléter une suite numérique telle que ci-dessous, l’élève va être amené à analyser les différentes relations existantes, tester les régularités. Il n’y a pas une réponse exacte mais bien un espace d’invention de règles de construction s’appuyant sur des observations diverses.

3. L’étude des motifs favorise la pensée algébrique et algorithmique
Lieven Verschaffel, dans le cadre de la conférence internationale du CSEN de 2022 « mathématiques pour tous,[iii] rappelle que, selon de nombreuses recherches en maths, l’activité de pattern (les motifs) précoce implique des éléments fondamentaux de l’algèbre :
- Comprendre qu’une chose peut en représenter une autre
- Utiliser des noms pour étiqueter ou identifier des motifs
- Rechercher des règles et des généralisations dans divers cas
- Prédire un comportement fonctionnel
La pensée algorithmique, quant à elle, se définit comme la capacité à résoudre un problème en structurant sa solution par une suite d’étapes et de règles précises.
Dans cette optique, si on se réfère à l’activité citée précédemment « compléter la suite de nombres », il est intéressant de demander aux élèves de citer un élément éloigné (exemple : quel sera le dixième nombre, le centième?) permettant ainsi de mettre en défaut les procédures de type récurrence qui deviennent trop coûteuses en temps. Pour déterminer le dixième élément, une variété des procédures de calcul des éléments peut apparaître pour une même régularité suivant la manière dont les élèves déconstruisent / décomposent le « motif ».
Aussi, pour être pleinement efficace, le travail sur les motifs doit être accompagné d’un enseignement explicite[iv], basé sur l’examen des régularités existantes, des structures et l’intérêt de s’en saisir pour établir des projections.
[i] Note du CSEN n°10, juin 2023
[ii] Piolti-Lamorthe C., Roubin S. et Trgalová J., « Des patterns dans les classes ! », in APMEP Au fil des maths. N° 547. 22 mars 2023, https://afdm.apmep.fr/rubriques/opinions/des-patterns-dans-les-classes/.
[iii] https://www.reseau-canope.fr/notice/le-developpement-et-la-stimulation-des-capacites-mathematiques-fondamentales-precoces-le-cas-de-la-structuration-mathematique.html
